Il calcolo della sfera e le piramidi di Giza. La geometria degli Egizi

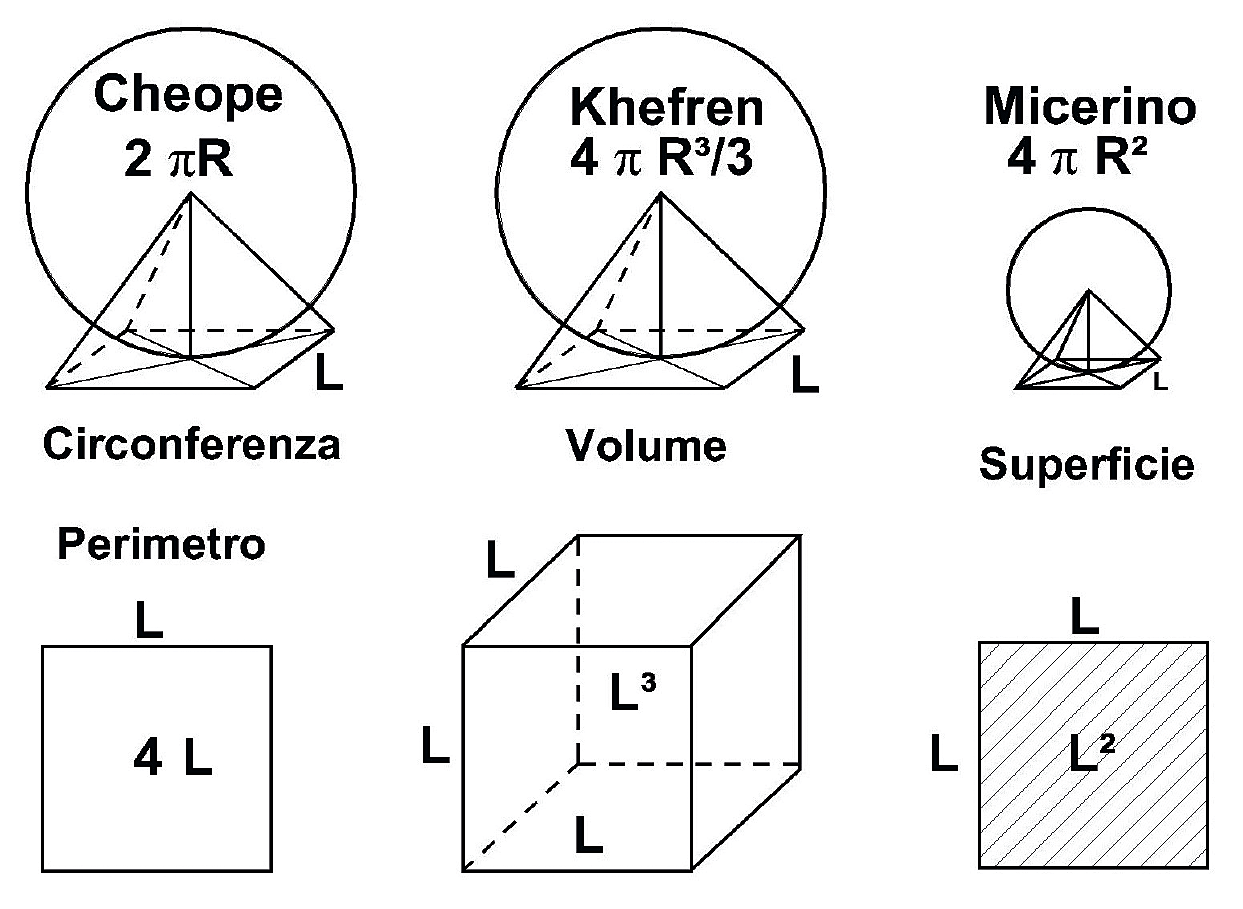
Le grandi piramidi egizie nascondono delle informazioni matematiche, cosa fino a oggi negata dalla maggior parte dell’egittologia ufficiale, ma sempre più evidente. Gli Egizi volevano infatti tramandare ai posteri, in maniera perenne e indelebile, i concetti di base della geometria e della matematica da loro conosciute e che facevano parte integrante della loro “conoscenza segreta”. Misure nelle piramidi. Le misure delle tre grandi piramidi di Giza rivelano, oltre a molti altri aspetti, che gli Egizi durante la IV dinastia sapevano calcolare la circonferenza, il volume e la superficie della sfera, ben 2000 anni prima dei Greci. Una conoscenza che per ragioni sconosciute fu dimenticata per millenni ₁. L’unità di misura di base delle grandi opere egizie è il Cubito Reale che equivale a cm 52,36 ₂. Questo valore è ormai comunemente accettato da tutta la comunità internazionale dei ricercatori del settore.
Molto rovinate dallo scorrere del tempo (tempeste di sabbia, piogge, terremoti, devastazioni), le piramidi hanno perduto quasi completamente i loro spigoli che sarebbero serviti per una verifica puntuale delle loro misure. Ricomporre le loro misure iniziali non è semplice, ma attraverso tutta una serie di controlli incrociati e di ipotesi basate su riscontri reali, si è arrivati ad avere informazioni abbastanza attendibili.
Gli antichi Egizi hanno lasciato scolpite nelle pietre delle loro meravigliose opere gli indizi della loro conoscenza approfondita in merito a molti concetti geometrici e matematici. Tra queste la capacità di saper calcolare le dimensioni di una sfera. Per dimostrarlo, è necessario analizzare le principali misure di quattro piramidi:
 

 
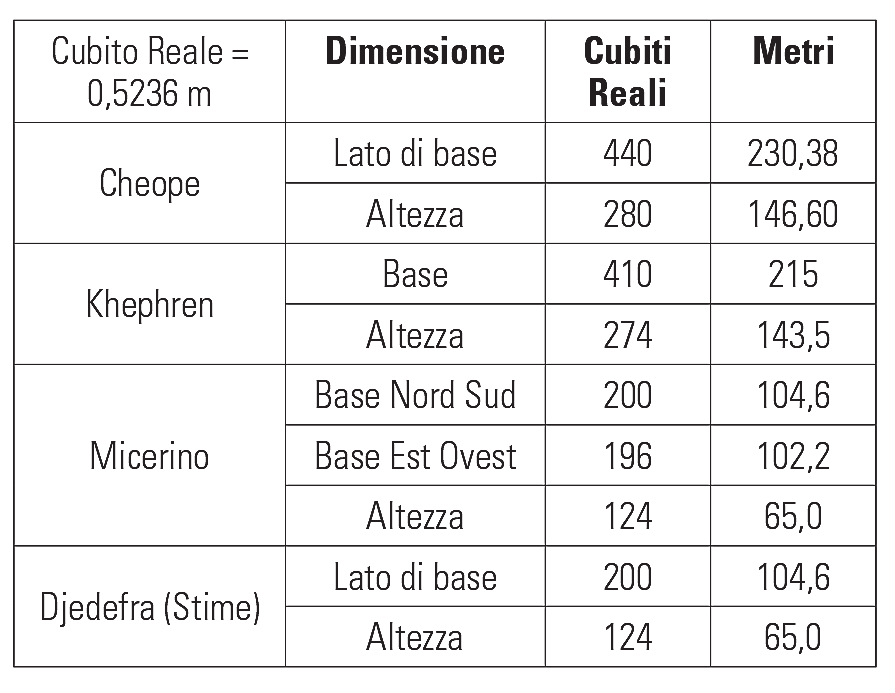
L’egittologo inglese John Edgar scoprì che il perimetro di base della Grande Piramide equivale ad una circonferenza che abbia come raggio l’altezza della piramide stessa (fig.1).
• Perimetro piramide in metri: 230,38 x 4 = 921,52
• Circonferenza: (146,60 x 2) x 3,1416 = 921,11 (scarto 0,05%). Quindi la Grande Piramide contiene innegabilmente il concetto e il valore di Pi Greco.

 
Partiamo con il considerare il lato di base della Grande Piramide (230,38m) come fosse un’unità di misura. Con questa misura, possiamo calcolare sia l’area della base della piramide stessa, sia il volume di un cubo che avesse il lato della stessa lunghezza.
• Area di base di Cheope: 230,38 x 230,38 = 53 074,9 m²
• Volume cubo con stesso lato: 230,38 x 230,38 x 230,38 = 12 227 405,6 m³.
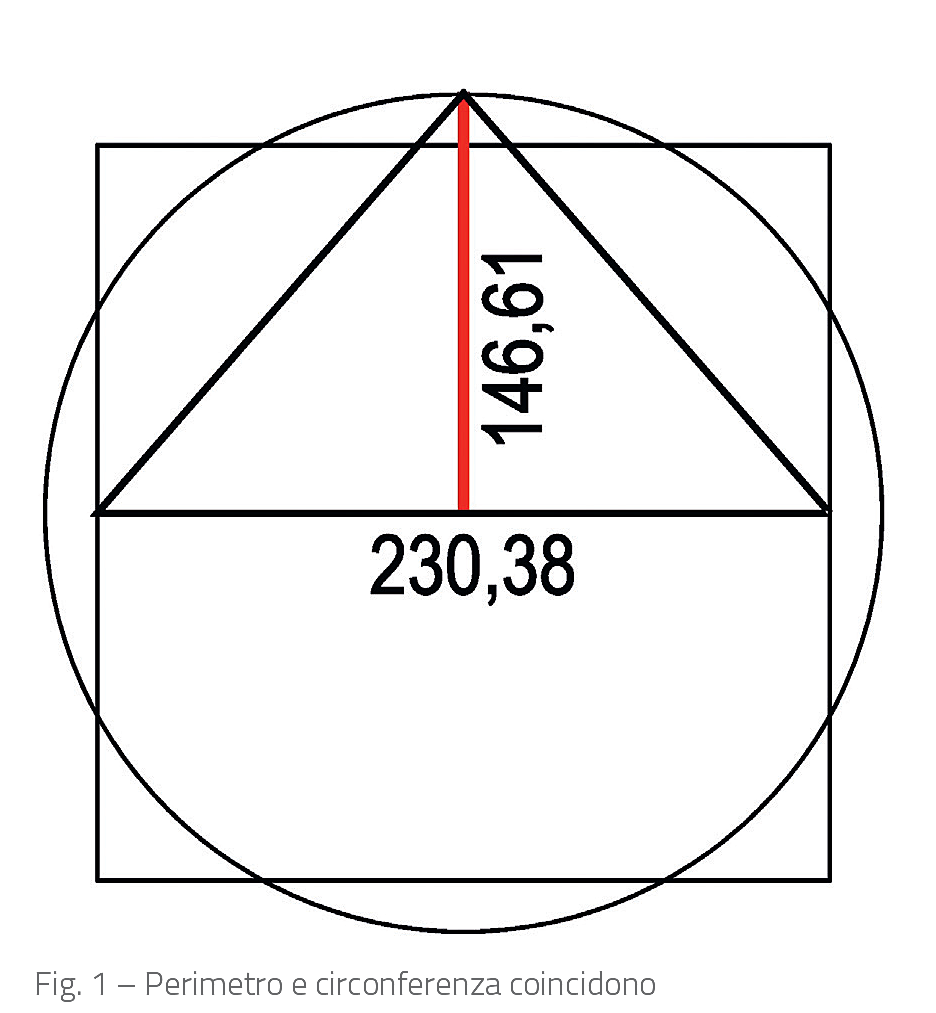
Ora proseguiamo, considerando le altezze delle tre piramidi di Giza come altrettanti raggi di tre sfere virtuali, ecco le tre corrispondenze con Cheope che si palesano: (per capire meglio come funziona il meccanismo, bisogna osservare anche la figura 2)
• Il punto A: la circonferenza calcolata per la base della piramide (2D) vale anche per la sfera (3D);

• Il punto B: la differenza di volume tra la sfera di Khefren (12 377 785,2 m³) e il volume del “cubo di Cheope” (12 227 405,6 m³) è pari all’ 1,2% quindi trascurabile; • Il punto C: la differenza di superficie tra la sfera4 costruita con l’altezza di Micerino (53 093 m²) e la superficie della base di Cheope (53 074,9 m²) è pari allo 0,03%. I due risultati sono quasi identici.
 
 
 

 
I calcoli valgono anche per la piramide di Djedefra? Djedefra, anche lui faraone della IV dinastia, costruì la sua piramide ad Abu Rawash a Nord-Est di Giza. Le misure di quella piramide, oggi molto rovinata, sono state ricavate dopo gli scavi: base di circa 106 metri e l’altezza tra 57 e 67 metri. Applicando lo stesso ragionamento fatto per la piramide di Micerino, questa piramide potrebbe fornire misure di una sfera con un volume uguale (o molto simile) al volume di un cubo con lato pari a quello della piramide. Supponendo una base di 200 Cubiti Reali (104,7 m) e un’altezza di 124 CR (65 metri), il volume della sfera sarebbe 1 150 349,2 m³, mentre quello del cubo sarebbe 1 147 730,2 m³ con una differenza dello 0,22%. In questo caso lo scarto sarebbe trascurabile. Per ora non si è mai trovato un papiro o un testo che spieghi come gli antichi Egizi calcolassero la superficie o il volume di una sfera. La formula per calcolare le dimensioni della sfera è dovuta ad Archimede che probabilmente l’ha appresa proprio in Egitto. Il fatto che su tre piramidi vicine geograficamente, storicamente, artisticamente e costruttivamente si possano incrociare questi dati, non può in nessun modo essere casuale ₅.  ■
 

1. Per una ragione di correttezza tengo a dire che una buona parte delle dimostrazioni qui riportate, sono liberamente tratte dagli studi del ricercatore canadese François Poisson che ringrazio.
2. La lunghezza del Cubito Reale (CR) è in strettissima relazione con il numero aureo e il Pi Greco. Infatti il CR = π/6 (verifica: 3,1416/6=0,5236) e al contempo π - Φ² = CR (verifica: 3,1416-2,618= 0,5236).
3. Ricordiamo che il volume di una sfera si calcola moltiplicando per 4 il prodotto tra Pi greco e il cubo del raggio e dividendo il tutto per 3.
4. Ricordiamo che la superficie totale di una sfera si calcola moltiplicando per 4 il prodotto tra Pi Greco e il quadrato del raggio.
5. Si tratta di una “reductio ad absurdum” cioè una dimostrazione per assurdo, dove l’assurdità consiste nel non voler vedere queste evidenti corrispondenze geometrico – matematiche.